This Friday engineers are attempting to cap the oil well. In the comments are the latest updates. To watch all of the spillcams at once, click here or click here and finally here.
This process is ongoing and even if it fails, frankly there is no other option but to continue trying to cap the oil spill. Below is an animation of the process:
Firstly folks, pay attention to engineers and experts. There is a lot of noise out there on the oil spill and frankly in watching the spill cams, I periodically shout out loud what a bitch! In other words, it's clear this is exceedingly technically difficult. See these previous posts on the oil disaster, Even More Ado About Oil, More Ado About Oil and Much Ado About Oil for some of the technical problems in engineering 1 mile below the sea.
Just to show you if this latest attempt fails, engineers clearly plan more efforts. They literally have put concrete on the sea bed floor to lay all of their tools around. As you can imagine, needing to lower a saw a mile down in the ocean isn't exactly immediate access to it when needed. The engineers have at least 5 different caps on the sea floor currently to try to get a good fit over the pipe gushing oil. Be patient.
We also have new animated projections of the spread of the spill.
The true economic impact is starting to show as well as the environment damage. I won't display the many horrific videos and images of birds coated in oil, dying, smothering, fish dying and people losing hope.
Currently various groups are working on economic impact reports. They vary from $1 billion to $70 billion, all assuredly low-balled. The true economic impact is dependent upon the spill rate, the continuing flow and the total amount of oil leaked. Additionally it is dependent upon ocean currents as well as public perceptions (tourism). Most critical on economic impact is the clean up effectiveness and response time. It's possible the spill will cause a double dip recession.
The Democratic Policy Committee put out a snapshot last week pegging the Louisiana commercial fishing economy at $2.4 billion and the Florida tourism industry at $60 billion. The document said economic damage "will be significant," citing reports of 70 percent declines in hotel occupancy along the Florida panhandle over Memorial Day and other signals that tourists are being spooked.
In the interim, let's just hope more boats scour and shower for oil soaked animals and life that can be saved.
The first relief well was at 12,090 feet yesterday, supposedly on track to be completed by early August. The relief wells are the known permanent solution to stop the leaking oil.
Another site covering the spill source containment efforts is The Oil Drum and they are moderating the comments to keep the noise down.
Consider this post the oil open thread.

Comments
2:42 CDT 06.04.10
Since unfortunately there is no running engineering commentary on what is going on in the most addictive spillcam, again, click here to watch them all in one page, here's the latest visuals.
I've seen a cap #3 being hoisted up from the sea floor. The cap currently on (I believe) is #4.
At the same time, we see some chaining going on seemingly to a pipe, but that might be cap #3.
At this time, it's clear the pipe is not attached and earlier we saw a lack of stabilization in the cap #4 position on the top of the BOP (the sliced off pipe or leak point).
So, my guess is they are switching to cap #3, which looks of a smaller diameter and a narrower pipe at the top (go figure on that one).
Why they gave up on #4 so fast who knows, except it didn't seem seated and stable on top of the BOP from watching spillcam.
The above animation in the post does show they have to let things stablize, take some readings, make sure it's not forming hydrates and clogging, get the gas out of the pipe, attach it, shut off additional values on the cap and so on.
So, I don't think anyone should reach any conclusions by watching a video snapshot yet.
House Energy Subcommittee
Here are some BP presentation documents about what went wrong leading up to the disaster. There is quite a bit of information with assuredly a heart wrenching hearing tomorrow on the environmental impact.
I personally cannot look at those photos of animals drowning in oil and dying.
The above link has some good diagrams for more details on what we're looking at.
I guess we're really geeking out here, but considering the entire disaster impact is dependent on stopping the flow plus clean up, I guess that's ok.
OcKham's Edge on the BOP and Controls
As I read the BP testimony, the electronic controls on an BOP depend on the rig and platform and its command and control being intact. Set fire to the rig and platform and you lose control of the BOP, and turn the BOP OFF.
This vulnerability was known to the Oil and Gas Offshore platform industry since at least 2000. In that time frame, I became aware of North Sea platform whose controls had to be re-initialized with different date routines to 'fix' the Y2K bugs.
These fixes created future year routines to allow for 6 character
dates. There is no removing a BOP as we can see.
Burton Leed
but something failed
that's what i read, it was supposed to do an automatic shut off but didn't.
and that included disengaging the riser pipe.
I just turned on spill cam and things look the same to me, but it's hard to say. Anyone see any piping or values shut down?
hard to know what's going on right now in spillcam
Because there are obstacles around the actual oil spill, it's hard to figure out what percentage of oil they are getting or if it's all billowing out. It doesn't look good
and it appears a lot of the woe is not getting that clean cut on the pipe. It needs to fit and seal.
I still haven't found a good technical answer as to why they didn't try to get a better cut on the pipe.
We'll see, seemingly they have all sorts of stuff to continue working on the seabed floor, but it sure seems that pipe cut is a huge problem. (unconfirmed).
One thing is for sure, if this is failing, there is no way they are going to announce that until way late in the day. Kind of our Friday Bank failures so markets do not immediately react.
closing of vents
Supposedly there are 4 vents on the cap, which we noted earlier. I guess what's going on is they are taking readings, seeing the volume getting up to top side and other metrics to then make adjustments.
The vents are not closed, so ya know, looking at spillcam and just the flow, we really cannot tell what's happening, beyond oil spewing out of the cap.
There seems to be some new activity, something coming off the seabed, but it looks like a box.
If someone finds a tweet or blog doing official real time updates on what's happening, let me know.
It's astounding I cannot find a few engineers somewhere using social media for accurate real time updates. They must be on the unemployment lines or scared shitless by some non-disclosure agreement where they are working (sic).
more spillcams added
Some of the spillcams the video quality is out. That's probably load on a particular stream, so I added two more links with feeds all one one page.
Supposedly, with vents open, they are collecting 1000 barrels of oil. They reported they believe they can capture 90%, but that said, we have various spill rates going on.
Not clear on these "experts" thing?
"Firstly folks, pay attention to engineers and experts."
HUH??? What engineers and experts? You mean those unvetted ones the oil company offshored their jobs to?
I heard one Indian "expert" extoll BP's topkill method, which I predicted was doomed for failure -- and while I am not expert, nor particularly knowledgeable on petroleum engineering, I can remember the facts and history behind processes and companies.
And, especially, I pay close attention to those with a track record of being correct on specific subjects and areas.
When I see some real experts and engineers, I'll begin paying close attention!
As it is, anyone suggesting the use of nukes in close proximaty to methane deposits, which could conceivably cause a mass extinction event, is clearly no expert on anything!
better than Cable hysterial pretty people
I've seen a host of absurdity on cable about this.
But that would be MOST amusing. Did BP labor arbitrage their engineers, fire the real experts and replace them with H-1B cheapos, moving on the contract deals and ignoring the fact they have no clue, but they sure are cheap?
When I say experts, I'm talking about various U.S. research institutions, Professors as well as U.S. engineers, not necessarily BP.
On the entire top kill, I was giving it the benefit of the doubt, because I am not an oil/mechanical/underwater engineer, it sounded absurd to me, I don't understand why they would not use chemical agents that would slowly expand and solidify in water, I know those exist...
but on this latest adventure, you've got some real idiots on TV thinking the oil will just "stop", haven't even read the procedure, cannot identify even a cap the BOP or a vent on the spillcams.
So, that's serious misinformation. So was that Matt Simmons who I kind of did a long lead in to say that.
But seriously, anybody know if BP is a huge global labor arbitrage agenda like Intel, HP, Microsoft, IBM?
I wouldn't trust IBM to screw in a lightbulb anymore and unfortunately they are still getting and get huge government contracts. Very scary.
upper limit top side 15,000 barrels a day
That's if they can capture enough of the oil, but that also means the top side capacity cannot handle all of the oil out of the well. I guess if they manage to capture any significant amount they could deal with that limitation.
Oh gee, Obama gets mad
Who where thinks that was staged, part of some political manipulation claiming Obama had to show emotion to save his political ass?
Sigh. Maybe those contractors will get cut a check. Which reminds me that stiffing of contractors is very common and done by large corporations who one would think they pay their bills. Why do they do this? Because they can. There is little legal recourse for a contractor to get their pay because they are considered a business, thus not protected.
I may be hallucinating but
spillcam looks like the oil flow out of the cap is slightly less. Anyone else taking a look and seeing any new activity, like a closing of a vent or a latch pin and so on?
It's not much less, just slightly to me. But who knows, this thing is almost hypnotic and I wonder if I'm getting hypnotized into wishful thinking.
robot arms on the move
These guys seem to work at night, which is scary for I sure hope they are not 1-800-Bangalore!
Although they might be waiting for cable news to go off air too. Cable news goes nuts the minute anything is seen happening on spillcam with a lot of misunderstanding. It's Oceaneering doing all of those operations, not BP, although assuredly a team of engineers from at least BP and hopefully all over are top side some place analyzing all of the goings on.
Ok, it looks like they tried a new cap, #7, then they are fiddling around with seals at the bottom of the top hat.
The pressure values are open, which means it's spewing oil but they are focusing in on the seal at the bottom, trying to get it sealed and it's really hard to tell what exactly is going on, but it looks like the gush is going out the bottom and the seals aren't working.
Seems what they are doing is trying a cap, taking a lot of measurements, tweaking a few things, stopping, analyzing and re-engineering on the fly.
Which they have to, actually engineer on the fly since no one has attempted this and they are assuredly learning as they go along.
You can see them analyzing the structures because the cameras are moving around.
Bottom line, the cap is pouring oil.
BP reported gas/oil collections
There are various estimates on total flow, typically 20,000 barrels a day but the real rate, which I wish they would measure, live on spillcam, so this guessing game can stop, is unknown.
It's pretty clear there are a host of variables they are having to deal with, plus not freeze up the pipe and the seawater itself is cold, which can cause hydrates to form and clog everything.
But assuming BP press people aren't lying (and clearly there press/marketing/public relations teams are quite the twister people)...
I know the relief values were open yesterday, not closed and they are a good diameter size, so if all of this is true hitting a 25% capture rate on first pass isn't too bad.
Sure there is crap spewing all over the gulf, but this appears to be an iterative process.
hydrates
I could be wrong in checking in on spill cam but it looks like they might be dealing with hydrates forming again. I'm seeing what I believe is frozen gas particles around, a lot of 'em. They are just firehosing disbursements down there too, so maybe it's a molecule formation happening, but it sure looks like hydrates from spillcam.
Last report is they are using one of the most least effective and highly toxic of them all top side. Dunno what is being used at the leak source, 5000 feet down.
That said, I wouldn't freak out about this for it's clear there is a balancing act going on on the sea floor and I suspect this is going to be baby steps, two ahead, one back, and so on trying to capture a larger and larger oil percentage.
There is also an amazingly amount of gas and that's highly volatile.
Reports are the relief well is faster along than August, but that said, there are hurricanes plus a lot can go wrong in drilling a relief well, kind of doing an elephant through a keyhole in terms of the target area the drill must hit.
anybody reading this turn on your spill cam
It looks like they are shutting off a value. I sure hope it doesn't freeze the damn thing.
I maybe hallucinating part 4, section b, part 6
I think that shutting off just one value greatly reduced the spill amount. I could be wrong and now it looks like they are checking all of the pressure gauges they have placed around and on hoses, but it sure looks reduced, I can make out the cap when before on Enterprise you couldn't see any of it and the other two plumes on camera appear to be smaller 2.
I have no idea why we don't have a least official running tweets as commentary on what's going on or at least some Academic doing that. I'm so surprised for this would be the mechanical/engineering spectacular I would think.
James Cameron
Cameron appeared on Hardball. Said he offered expertise from Academia and other Oil Patch experts. There is plenty of talent and ideas if they would deploy it. The entire problem resolution was single threaded.
Both Cameron and Cousteau offered deep water submersibles to BP and the U.S.
Neither the U.S. nor BP own deep water submersibles. As late as the 1969s there were deep water submersibles as Military assets
Burton Leed
Cameron also came on HB
and admitted his claim they were a bunch of morons was "wrong" and that they had the right gear, the right ROVs available.
I mean I was never impressed with "top kill" and some of the other stuff suggested originally but now it looks to me like they are more "on it" in terms of trying to architect/engineer using the data they are seeing, on the fly vs. "throw golf balls at it". I mean originally some of the engineering ideas looked like panic, almost pure panic vs. using the data to architect out something that had a prayer's chance. I wouldn't say that's true at this point though.
On the cleanup/containment side, that seems to be another story, I think they should be doing a massive engineering effort to suck up that oil, at the site, top side, some sort of gigantic collections via vacuums, pumps, etc.
But Cameron is an underwater film maker (now a 3D one), not an underwater engineering guy per say and this is really coming down to mechanical/oil engineering.
I'm not impressed with some fancy filmmaker coming on national TV and calling a group of engineers are bunch of morons when he doesn't know what's happening. I know these guys (where are the ladies btw?) are under enormous stress and one does not think clearly when there is that much pressure. Insulting them assuredly didn't help things, esp. when you're relying on people to use their wits, on the fly, to figure out ways never been tried to stop the leak.
It's Oceaneering that's clearly doing at least all of the underwater ROV and deployment stuff. That's a contractor to BP, not BP itself. You can see their hats and titles on each spillcam, (there are 12 spillcams) even the task that's happening now, they are putting titles on the video stream.
I've been wondering about the Navy. I know they have submarines and all sorts of stuff to go deep and then there is that lovely nuclear bomb retrieval issue at the bottom of the sea, along with sunken submarines, so where's that technology and could it be applied?
All of that said, I'm watching spill cam right now, just watched a robotic arm spend a good 15 minutes trying to latch onto the knob to turn off a value in the middle of a massive velocity oil gushing force which makes the entire screen go black so you can't see shit. I mean at least 15 minutes to make 1 90 degree right turn on a knob.
Another time it was like a half hour watching them untie a knot in some tubing/cabling. It's clear the conditions are extreme, even taking under consideration these are robot arms, manually controlled.
I mean I can see some technology that needs to be added pronto, #1 being 3D cameras, #2 being touch sensitivity sensors to the robotic arms...
Does Cameron have 3D Cameras that do not require blue suits, reference points in action but truly can coordinate the images to create 3D in real time in that mess/junk down there? I do not know, I honestly do not know if that issue has even been solved, to image process multiple cameras, with absolute reference points computed, on the fly, in real time, plus produce a real time accurate 3D image. As far as I know filmmakers have to reference position, which is why you see actors in leotards with little ping pong balls attached all over it. Those ping pong balls are the absolute position reference points.
but in terms of stopping this well, it looks like a massive hydraulics, avoiding freezing, velocity, flow directions, interactions with deep sea pressure nightmare frankly, assuredly out of my pay grade. and I don't see what kind of submersible technology can deal with that one.
I see some vacuum technology maybe, piping it up to a ship, oil rigging stuff...
Anywho, this is one of the reasons I decided to keep oil open threads going on EP, to put the focus on real technology because there are just way too many people, who really do not know what they are talking about, all over the place and some of it is true misinformation.
It's bad enough one has the barracuda BP PR machine on full throttle.
Cameron is an Idiot
I wish they'd have given him a shot if only so he'd have fallen on his face.
Cameron knew his offer wouldn't be accepted but he got the publicity he wanted out of it.
One side of BP caused this and an entirely other side is trying to fix it. The idea that Cameron would know anything about sealing a highly pressurized reservoir of oil a mile under the water is ludicrous. If his help was needed then the US government should have accepted since they are 'in charge'.
The Navy probably has the equipment to at least attempt a fix but I'll bet politics wise they don't want to own this and give BP an out either.
Most of the ideas that involve increasing pressure in the BOP seem to be rejected out of hand from a fear that the BOP will simply 'break' and make things worse or involve not having enough muscle to do things down there such as removing a flange and installing a new fitting.
If they completely removed the BOP they could put a plug into the pipe on the sea bed but that would be filled with a lot of 'what ifs' which scare them.
BP is toast and its all about damage control right now till someone buys them out.
not so sure they could remove the BOP
Something about the damage and a live well, but I cannot remember the details or where i read them. If you dig it out, link it up. I'm finding the best technical discussion is the oil drum.
While the bad guy du jour is BP, all that has happened is they usurped Goldman Sachs, who dethroned Citigroup, who took the heat off of Microsoft...
I mean they are all sociopathic feudal kingdoms who pour way more money into "messaging" and lobbying than actual solid engineering and their core business.
I mean it's ridiculous, the engineers beg for money in comparison to some idiot who "manages image and messaging".
This time though I think the focus on BP being evil (of course they are evil! They are the 2nd (?) largest corporation plus an oil company!) is almost adverse to working on getting this solved and cleaned up.
It should be more BP cough up the money now, BP, let the super tanker in now, BP put more bird rescue boats on the water now, BP give this wildlife refugee more money now and so on as the focus.
Clean Up is being Shortchanged
They should be spending much much more on cleanup than they are. That area should look like its being invaded by clean up workers and clearly it doesn't.
wildlife dying in mass now
I cannot handle looking at those photos, it just breaks my heart and I knew this would happen, but now they are seeing massive dead birds, wildlife, dolphins, you name it showing up for miles and miles.
I about cried when I first looked at the real spill rate estimates, knowing this would happen and I wish they could pick up every single living thing and relocate all of them.
It will make you cry to read the stories so I'm not posting links, just because it's so upsetting just to know it's going on.
Has Anyone Calculated the Economic Effect on the Southeast?
Whats all this going to cost?
The fishing industry will be dead there for decades and thats multiple billions per year.
Area employment will be affected for decades.
Area housing prices will be affected for decades.
Area tourism will be affected for some time.
Area taxes will have to go up because tax revenue will fall.
This could cause a shift in the population away from coastal areas.
an EPer emailed me offline
saying they were working on this so I've held off. But I've put up a few posts on this, the latest numbers I saw were from the DPC @ $70 Billion.
I am game to go into the regional economic databases via the BLS and the Fed and plain number crank what we believe the real losses to be. You can take the entire fishing industry of the gulf, the tourism industry, hotels, then, if they continue the ban on offshore drilling, that's a huge, there are all of the support services, the workers, and plus the secondary effects with consumer spending crashing because people don't have jobs...
I think those are the biggest sectors, so it's a matter of tallying them up for the entire gulf region from New Orleans East (I think the currents and wind all mean the oil goes east and south).
There might also be issues with additional shipping of unrelated things, New Orleans is a major port, have no idea about the general state of shipping lanes in the gulf.
Bottom line, Hurricane Andrew was about $41 billion, Katrina was $90.3 billion
but that's massive infrastructure damage, I don't think the fishing industry was that damaged long term.
Anyway, I just don't buy only $70 billion if it turns the entire gulf coast into an oil slick and kills everything in it's path.
Detailed Analysis Will Be Valuable
There will be plenty of lawsuits and the states want them all heard in state courts so the Feds can't throw out punitive damages the way they did for Exxon.
I'm sure a good analysis will be worth its weight in gold to the plaintiffs. Food for thought before you or who ever publish something a bit too detailed.
Funny JP Morgan Chase created the credit default swap specifically for Exxon, it ends up helping bankers kill the world economy and then the courts throw out punitive damages nullifying its original purpose (cds).
new flow rate analysis attached
I attached the latest estimates on the total amount of oil spilled and the current spill rate.
Despite the big paranoia out there, frankly, the people on this team is a bunch of geeks and I think this is a valid estimate and document, even if HuffPo wants to get all flipped out about it.
It's probably 20,000 barrels a day and believe this or not, I see various ratios out there on what makes up a barrel. It's 42 gallons, end of story. It's not 72, it's not 52, it's 42.
Damage to BP
This is a company that tried to morph into a "green" company. You can flush that down the toilet.
Their brand has become toxic.
People are refusing to buy from their stations. If people are pissed off enough, this may be a bigger problem than they can solve.
Frank T.
Spillonomics
A good article talking about how bean counters not only labor arbitrage workers but also cut corners on safety with our favorite "rare event" modeling.
New York Times article on it (but not in depth enough on cost management analysis).
Yet Another Superficial Analysis from the Times (Magazine)
"For all the criticism BP executives may deserve, they are far from the only people to struggle with such low-probability, high-cost events."
Let's look at the history of industrial safety for a moment. Workers on Erie Canal, Tran-Continental Railroad, skyscrapers, Deepwater Horizon workers did not make a free, informed choices and paid with their lives.
In purely economic terms, the choice is not rational. You and I and other readers know that this is because they are not 'liberated'. Others see the choice to work for low compensation and high risk as a modern form of slavery.
Times looks at the issue from the standpoint of capital, not lives or environment. Once you open these discussions up, you get to the heart of how this economy really works, and its flaws.
Burton Leed
good point
That is the heart of the matter. The only thing that is dictating decisions is that quarterly profit report to Wall Street and lining their own executive pockets.
We've had some great policy recommendations to change corporate governance and executive pay compensation.
The real problem is our government. The American people have been royally shafted by our elected representatives, that's Obama on down. Health care reform is a joke, they did not reign in insurance companies or costs, financial reform is a joke, they did not stop TBTF, it looks like what is there on derivatives will be ripped out, they put a consumer protection agency under the Federal reserve....
Even Stimulus, money poured overseas, they did not do a direct jobs program....
On pretty much every issue the people lost and the Lobbyists won.
BP reporting a 10,000 barrel a day capture
The estimates on the spill rate vary widely, which is why I attached the latest report so you can see the methods and the details and the disparity. I'm going with at least 20,000 barrels a day and assume that's a minimum so this means, if BP isn't lying, they hit a 50% collection rate with the cap.
That's pretty good really all things considered. It's obviously a tuning game, dealing with pressures, stability and so on, I've watched them on spillcam continually "tune" it to try to collect more.
I think they need a second system.
That said, I just checked spillcam and right before the videos went off line, I could see the cap moving. It's a pressures/freeze game they are playing, truly a bitch.
Last reason I saw on why they cannot remove the BOP 5000 miles below the sea with a gushing well is it's too dangerous and it might all blow up. The details I do not know.
look at this dinky screen!
The guys controlling the ROVs, jesus, haven't they heard of HD large displays? The resolution doesn't even look HD either, never mind higher, and we know the full video you cannot see jack due to the plumes of oil often.
Get these guys some high resolution 24", 32" displays man.
they ran out of room on the ship collecting oil
I'm assuming that they had it planned for 15,000 barrels a day already which is supposedly what the ship could process so the fact they ran out of room
is a very good sign!
I also watched one of those mechanical arms trying to get a socket wrench around a bolt to the point you would assuredly either need valium, or throw the computer screen across the room.
Seriously, trying to fit a socket wrench on one bolt went on for hours.
this is why some people should not be listened to
We have these sorts of posts, pointing to what they believe is "gushing" oil to "prove" BP is lying and the cap isn't working and yes this is a published article.
Yes, it looks bad. But the base of the cap is 4 feet in diameter. it's difficult to know the volume and density of the "gushing" oil outside the cap, but safe to say it's less than what is inside of it. That's bouncing off the cap walls and out. The plume looks huge but contained within is the cap itself, one cannot assume that plume is spherical in volume, it's not, it's a "ring". That is the visual illusion folks are freaking out on.
It's in the diameter of those fins, which from the cap dimensions are much less than the diameter, so in other words, it doesn't look to be 4 feet of pure oil, in a ring, outside the cap.
They also do not have the relief valves shut. There are 4 and they have only shut one. the reason is pressures and make sure the entire thing doesn't fall apart and they are back at square zero or worse.
They also are pumping so much oil they had to get more ships and add more "oil trains" to cart it out than they prepared for.
Unless BP is lying, which wouldn't be unheard of! (ha ha) assume it is capturing so much oil they had to line up new drilling ships and tankers to cart out the oil.
But bottom line is the most one can say is there is a butt load of oil escaping from the cap, but the total percentage, one cannot say without knowing the volume area of that "gush", the density and then the internal press/velocity and volume going up the pipe and at what rate.
How Much Can They Capture?
Its a 6 inch pipe over a 21 inch pipe. How can they get 80% of the oil? I'd say they are getting 100% or there about of the gas coming up though.
6" vs. 21" vs. 4'
I'm just not that well versed in fluid dynamics to know but I have watched the intense debate going on at the oil drum over this. To me, the velocity would just increase, but what is the maximum flow rate and does that go against the limits of the total spill rate before the cap? At 1 mile below the sea at 2600 PSI? I've yet to read a credible answer, I guess I could crack a physics book if you see some "plug in yer numbers" formula somewhere.
latest updates on spill containment (at source)
There is a real question on the true flow rate out of the broken BOP. Firstly, BP ran out of production capacity, which is 15,000 barrels per day (bpd). This means either BP didn't believe their cap would work, or BP itself is grossly underestimating the spill rate.
I took as the absolute minimum 20,000 bpd, but obviously designing for the minimum is not wise if one plans on capturing > 90% of the spill amount.
They have pressure gauges sensors now all around that BOP and cap. Also, those ROVs are each equipped with Sonar. Assuredly they could put some measurement sensors somewhere in the stream and find the true spill rate. I have no idea why they don't that, but maybe they believed their own denials and thus designed for a low spill rate.
Even now they are shooting for 20,000 bpd capacity, but is that really wise and shouldn't they be preparing for at least 30,000 bpd?
There is a massive amount of gas coming out of the well. It seems they have no other solutions but to burn it off at the surface. These are some scary pictures watching the controlled gas burn from the ship.
Right now, they have more of these caps moving to the sea floor. It looks like they have taller valves, closures on the valves that can be remotely controlled (which if you watch a mechanical arm try to close a value, that sure sounds more efficient!) and a host of new sensors and pipe heights. So, it looks like they are learning from their current cap design and doing redesigns top side to improve efficiency.
In other words, they are mechanically engineering new caps as a result of what they are learning about each attempt. This truly is engineering on the fly, anyone with a technical background can tell that by watching them through spillcam.
On the current cap, with 3 of the 4 vents open, just one vent closure increased the oil capture rate by 600 barrels per day. Last report was 11000 bpd and that is when they exceeded production capacity top side. Recall them must separate out seawater, gas, whatever from the actual oil before storage. That's not to make $$, that is to make sure they do not blow themselves up.
The more you let oil not escape, i.e. close valves, the more the overall force of the gusher grows, the pressure grows and potential hydrates can form and so on. The cap weight is 2 tons and is loaded with lead, trying to counter the force pressure net of the well vs. the sea pressure.
This is why it's an iterative process. Last thing you want to see is that cap get blown off by the gusher force itself. Or worse, it gets clogged.
Why I am focused so much on the engineering of this effort is all things are affected by total amount spilled and the rate.
It's the key thing, to stop the spill at the source. That should not diminish the efforts to capture the spill as close to the source as possible or to diminish the efforts to keep the oil out of marshes and all else that is going on.
The spill response is now massive, as if the spill, covering 4 states. Most of the wildlife recovered is already dead. They are putting up some nice images of pelicans getting washed and rescued, but for each lucky bird saved, it's a good 9 that are dead behind it (or more). Then there is all that one cannot see, a mammal maybe able to live counted in oil for awhile, but you can bet a host of other life, the minute the oil reaches it, dies and it's just falling to the bottom of the sea, you'll never see it.
While all are looking at the relief wells as the real solution, those too have had problems, so it's not guaranteed.
The good news is engineers are clearly in charge now and making some progress. Frankly the entire globe is dependent upon these cats figuring this out, which is why these oil open threads are so focused on the technical aspects and obviously highly supportive of their efforts.
Obama admits oil spill "economic impact"
To date we have had denial after denial after denial on the true economic impact the oil spill will have on the U.S. economy. Now Obama admits it will be substantial.
Recall Katrina was about $100 billion. The highest impact study we have to date is $70 billion from the DPC.
Yes, Katrina was a disaster, leveled huge sections of the gulf, all construction, roads, businesses, fishing boats and so on were wiped out.
That said, it was a one time event per say, you had mass destruction and then massive clean up. Oil isn't the same thing. It gets into the marshes, the food chain of the fishing areas, the oceans, the water and it's a nightmare to even get it out and that's just the surface stuff.
I think our best example on how to really model an economic impact is the Exxon Valdez on Alaska, which has affected the local economies ever since.
And just today I saw a justification for those of us "doom and gloomers" predicting a double dip just had residual negativity...i.e. we're just a bunch of bummer people.
uh, no, we have statistics, EIs and catastrophic events!
Don't listen to Matt Simmons
Dylan Ratigan just had these guy on again. Folks, we'll see but spewing crap on TV claiming there is a 2nd massive leak on the seabed floor, 7 miles away and they should 'blow up the well' and "this will never been stopped" and so on ...
well, frankly, you need to read real engineers, real oil people, real mechanical engineers, real geologists and real scientists to obtain real information.
I'm just not seeing anything to back up these MSNBC rants frankly and each time, this guy's credibility is going further down the pipe.
I mean the entire nuclear bomb thing has been debunked, re-debunked and further debunked. How many debunkings does it take?
My understanding is this guy is an executive, not an engineer, so I'm starting to find this stuff a distraction.
It's bad enough, getting real data, real facts on what's going on and throwing CT rants around just is not helping.
Ratigan would do everybody a great favor to have on his show independent experts, research Professors, engineers to give a better feel for what BP is really hiding as well as commentary on the current efforts.
7,541 barrels in 12 hour period!
From BP press release update, BP is reporting 7541 Barrels were collected from 12AM to 12PM, a 12 hour period. This means they are collecting over 15,000 barrels of oil per day!
That's great news people! There is also an astounding amount of gas coming up, in 12 hours, 15 million cubic feet.
Obviously the 20,000 barrels per day is assuredly a minimum spill rate, but they really need to get an accurate real time reading. There are fines associated with the spill rate and of course the Internet is claiming this is the reason we do not know, but looking at the designs, I'm wondering if the engineers do not have an accurate estimate either, because they designed for a lower overall flow rate.
Efforts to Minimize Leak Estimates
I have noticed (maybe especially on the Oil Drum) there are clear efforts to minimize the size of the leak in the first place.
Its certainly in BP's interest to have the public believe the minimized estimates since the fines they pay will in part be from that data.
The long time posters with info on the Oil Drum are either in the business or retired so their sympathies are also with BP. Thats clear from the tone of the posts from those users imo.
Certainly the media is mixed on this quoting everyone.
Its impossible to know the flow rate absolutely but the gas would be the first thing through that 6 inch riser now as opposed to the heavier oil.
Another thing that has been ignored is that not all oil is alike. This oil is VERY heavy dense oil with low viscosity that does not mix easily with water that should be obvious to anyone who sees it. I'm wondering what the weight of a barrel of this oil is versus the weight of a barrel that comes from Texas lets say.
There is still a huge amount of oil leaking into the GoM from what I can see anyway.
eh
How I found out about the fines being directly scalable to the real spill rate was on Oil Drum.
I think what you are reading is a lot of professionals in the field, so I wouldn't claim they are on the side of BP, they started by exposing peak oil and their agenda was to move to alternative energies.
I think they are simply analyzing the engineering as best they can because they are technical people for the most part.
But on the spill rate itself, if BP can put over 20 gauges they are obviously reading even through Cameras they could put a sensor of some sort and get a real flow measurement. After they sawed the pipe off, that's when they had a good shot to get an accurate rate, but honestly I just don't know. On one hand it would seem in BP's interest to low ball it as much as possible. On the other hand, they just underestimated the rate so much they did not have production capacity in place...which any delays isn't in their interests.
but all things arise from the spill rate, so it drives me nuts.
Myself, I switched into geek mode on this simply because I know all things follow shutting down the spill and I have the technical background enough to track and dissect.
Oil Professionals
I yield to their expertise but they are not above 'make it fit math' and 'I have experience so thats not true' to reach their desired conclusion and they are oil professionals whose livelihood is dependent on 'oil'.
There have been loud roars over any talk of stopping offshore drilling so the site may be about peak oil and alternatives but that doesn't follow to the posters I am seeing.
They debunked the estimates of anymore than 20,000 bbpd coming out of the well with 'wells aren't that big in the GoM' but the nearby BP Atlantis rig has a design capacity of 200,000 bpd processing capacity for some odd reason. I realize its surely over engineered but by 1,000% just in case or is it that wells of that size exist in the GoM? If that rig was designed for much bigger wells then it would be elsewhere.
some or all?
BP is reporting they are capturing 15,000 and so that's only 5k left for the spill out and frankly who knows, it's a circular "ring", a lot of increased friction, velocity with the flow bangin' around inside that cap before blowing out, plus they are spraying massive (probably toxic) dispersant right on top of the oil not being captured by the cap..
They have had a problem with trolls too. The oil drum was this niche site, similar to EP and now they are having to buy new servers like mad since this happened...
So, is everyone arguing that or some?
Just a Few
The best posters there are really neutral.
There was a post by someone who said they hadn't posted there in some time asking what had happened to the place. They'd been a member for two years (I checked) and they came out and said that BP had obviously planted some apologists there who were tech savvy.
Those would be the posters I refer to and no they are not the majority.
max capacity, production, typical production, spill flow rate
Jim,
I did a little digging around on throughput (for a CE term) on the pipes and so on, and frankly it all explains to me why Petroleum engineering is a specialization area. So many variables they use computer simulations to predict the flow rates. So, that's beyond me and also it became obvious, because there are so many different materials coming into play, it's not just pipe diameter, it's above my pay grade to try to estimate it. Unless I've got a prefab Matlab script around, I'm just too clueless to tackle it and am stuck with reading those engineers arguments I guess.
Then, I went looking for average production rates per well. I saw this and frankly the Internets are now "clogged" with crap about just the spill, I could not find out the original production of each well, in the Gulf oil fields where the spill is.
It appears that wells for the most part do not exceed 100,000 bpd and it also appears to be a good bet this one is about 24,000 bpd to 33,000 bpd.
BP just announced a plan to increase capture to 20,000 bpd and obviously they need to up their capacity topside ASAP.
Kind of amazing you cannot locate the per well maximum capacity in that oil field, maybe you can, but you know they know that, else they would not have drilled there in the first place.
I'm not kidding maybe in some gov stat site, but somewhere, per that oil field, has to be expected production, maximum production, but per well! Wikipedia, pretty all of your "just information please" sites are plasters with crap instead of these basic stats. Very irritating.
June 7th, 14,800 barrels 24 hour period
This is supposedly still with 3 of the 4 vents open. No idea when the production line, topside, will be increased. Supposedly there is another ship coming but ships mooovve sloowwly.
There are also reports of other leaks. The oil drum has a huge post on natural seepage. That said, there are some aerial views on some strange slicks, pointing to another well.
Frankly, I'll wait to see some credible verification what's going on, for that's just above my pay grade to ascertain oil leaks, how the slick forms and how it moves and how one ascertains the source point. We know for sure one puppy that is a massive gusher and that's the blown up well all of the focus is on.
BP CEO to testify before Congress next week
This is just so classic. There is incredible Populist outrage, so Congress gets a CEO to testify and then does a public tongue lashing and admonishment, doing their best to get on the evening news (The committee members). But....as we can see in terms of actions....there are none. We don't have one iota on executive compensation reform, financial reform is being ripped further asunder, (guess lobbyists don't like that cheese in their loopholes - swiss cheese, get it?), people are being foreclosed on, didn't stop that, didn't get more jobs, didn't stop pretty much anything.
So, la de da, we get another public thrashing with no real consequence.
CNN spill rate hysterics
This is getting fairly ridiculous for CNN is reporting the spill rate increased "exponentially". That's ridiculous, that's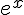 . I mean come on, these well have limits without any gear on them, just a hole in the ground.
. I mean come on, these well have limits without any gear on them, just a hole in the ground.
They need to get give measurements out here, BP is playing games with the spill rate and they should just cough up.
Pages